Allen's Blog

体制山下的泼猴

0%

每周导学-第十一周-统计学进阶

发表于 更新于 分类于 阅读次数： Valine：

Everything is difficult until you know how to do it.

Hi，同学们，上周我们学习了统计学基础知识，包括概率基础、描述统计学和推论统计学的基础知识，本周我们将会进一步学习推论统计学——置信区间&假设检验以及它们的应用之一A/B-test，在这之后，我们还会讲解一部分机器学习入门——线性回归&逻辑回归，与上周相比，这周我们会接触较深的理论知识，更多的代码，你可能会觉得学起来有些吃力，但请一定保持信心，你可以多次暂停观看课程中的讲解视频，跟着一起多动手，或者你也可以按照下面我给出的额外资料去查漏补缺，相信你们一定可以的！

项目四(P4)阶段总共包含三周，在这三周内，我们要对统计学进行学习，掌握基础的描述统计学理论、基本的概率知识、二项分布和贝叶斯公式，并学会使用 Python 来实践；学习正态分布、抽样分布、置信区间以及假设检验的概念和计算方式；学习线性回归以及逻辑回归，在真实场景中应用，比如分析 A/B 测试结果，搭建简单的监督机器学习模型。可谓是时间紧任务重，但是也别怕，统计学的基础知识还是非常简单的，跟着课程内容一步步来，自己多做笔记多查资料，一定没问题的！

那么我们的课程安排：

时间 学习重点 对应课程
第1周 统计学基础 描述统计学 - 抽样分布与中心极限定理
第2周 统计学进阶 置信区间 - 逻辑回归
第3周 完成项目 项目：分析A/B测试结果

本阶段可能是个挑战，请一定要保持自信，请一定要坚持学习和总结，如果遇到任何课程问题请参照如下顺序进行解决：

饭要一口一口吃，路要一步一步走，大家不要被任务吓到，跟着导学一步一步来，肯定没问题哒！那我们开始吧！

注：本着按需知情原则，所涉及的知识点都是在数据分析过程中必须的、常用的，而不是最全面的，想要更丰富，那就需要你们课下再进一步的学习和探索！

本周目标

学习课程中的置信区间 - 逻辑回归课程，掌握统计学进阶知识。

学习计划

时间 学习资源 学习内容
周二 微信群 - 每周导学 预览每周导学
周三、周四 Udacity - Classroom 置信区间 - 逻辑回归
周五 微信/Classin - 1V1 课程难点
周六 Classin - 优达日 本周学习总结、答疑
周日 笔记本 总结沉淀
周一 自主学习 查漏补缺

知识清单

置信区间

学习之前可以先回顾一下正态分布、抽样分布和中心极限定理的相关知识。

是什么

还记得上周用到的优达学生喝咖啡的数据吗？我们同样以此为例来探讨下置信区间是什么。

假设，优达的学生有数十万个（总体），而我们能获得的学生数据只有几百个（样本），我们通过做样本均值进行抽样分布，得到了一个近似正态分布的图形，但这也仅仅是样本的均值分布，也就是样本统计量。我们利用样本统计量的分布去构造总体均值（总体参数）的估计区间，就叫做置信区间。

有什么

  • 置信区间的两种应用

    • 刚才的举例中我们用得是“均值”，这算是利用抽样分布建立单个参数的置信区间，可以应用在单变量估计等方面；

    • 你还可以计算两种分类之间均值的差，这就是两个参数的置信区间，可以用在两变量的对比(A/B-Test)上，比如说医学上不同药物的治疗效果，不同广告的吸金率，不同网页的点击率等等。

  • 置信区间的显著性

    • 统计显著性：即我们通过理论分析得到的结果。在统计学上用α表示，叫做显著性水平，它表达的是区间估计的不可靠概率。比如说，我们获取了95%的置信区间，那么显著性水平α = 1 - P = 5%。

      一般的，显著性水平都要求达到5%即可，这在之后的假设检验中会学习到。

    • 实际显著性：即我们除了理论分析得到的结果外，还要考虑实际情况，比如说你能有多少资金用于投资，或者你的网站承载力能达到多少等。

  • 与传统置信区间方法的对比

    传统的置信区间/假设检验方法有很多，比如说t-检验、双边t-检验等等，但是我们所掌握的自助取样法可以代替他们全部，当然有一个前提条件，那就是你的样本容量一定要足够大，如果你的样本容量实在是少，那就只能选择传统方法去处理了。

    获取传统方法python代码的方法，请自行去Stackoverflow搜索。

  • 准确性&可靠性

    这里课程中翻译的有点儿晦涩，这里着重讲一下，我们以候选人A为例（在95%可靠性下具有34%±3%的支持率），大概分布可以如下所示：字丑就将就着点看吧。。。

    iVvVW8.md.png

    • 在上图中我们能发现，置信区间的置信概率（可靠性）越高，置信区间的宽度也就越宽，误差范围（准确性）也就会越大；那么当我们缩小误差范围时，置信区间的宽度和可靠性也就随之降低。
    • 结论：置信区间的准确性和可靠性是一对相互矛盾的标准，所以在实际工作中，只能提出其中一个条件，然后推求另一条件的变动情况，如果所推求的另一条件不能满足要求，就应该考虑增加样本容量，重新进行抽样，直至符合要求为止。

怎么用

课程中已经给出了很好的示例、问题及解答，在这里只是拎出一些面生的代码进行讲解。

1
2
3
4
5
6
#设置随机种子，能保证结果之后可以复现
np.random.seed(7)
#按百分比取值
np.percentile(array,q)#q介于0到100，取的是array中的q%位置的数。（从小至大排序）
#拓展——按分位数取值，其实效果和上面按百分比取值一样，只是q值的范围变了
np.quantile(array,q)#q介于0到1，取的是array中的q位置的数。

注意：置信区间和假设检验只关注的是总体参数，而不能对某一个体下结论。

假设检验

是什么

  • 基本概念

刚才我们讲解了什么是置信区间——为了得到总体指标，使用样本统计量去估计总体参数——这是一个从样本出发去研究总体的过程。

我们现在换一个角度，在实际分析问题中，能否去假定总体参数，然后根据样本数据，去检验这种假定是否正确，从而实现对总体指标的分析？其实这种从总体出发，用样本尺度去检验实现对总体参数分析的过程，就叫做假设检验。

置信区间与假设检验的关系：从上面的表述可以看出，假设检验和置信区间在本质上是一致的。如果使用样本数据对总体参数进行估计，在一定的置信区间下，总体参数就应该落在这个区间，如果假设的总体参数不在该区间中，则就有理由拒绝该假设，这其实就是从置信区间的角度去完成了假设检验的工作内容。

  • 名词解释

    • 零假设H0：一般的，零假设就是你不想要的结果，总包含等号。我们的目的就是要证明零假设是不成立的，是可拒绝的。比如说，你更新了网页设计，不想看到的是更不更新对你网站的流量没什么影响，那么零假设就可以这样设置。
    • 备择假设H1：一般的，这就是你想要的结果。注意，备择假设应该是零假设的对立。
    • 一类错误：原假设H0为真，却被拒绝。也叫拒真概率，一类错误是更为严重的错误。
    • 二类错误：原假设H0为假，却被接受。也叫受伪概率。

    在实际工作中，我们不可能要求一个检验方法永远不出错，但可以要求尽可能地减少犯错误的概率。但在样本容量给定的条件下，两种错误发生的概率必是此消彼长，因此，我们通常是控制第一类错误的概率，使它不超过某一给定的值（一般的取0.05），这样加以控制第一类错误，以此来制约犯第二类错误的概率。

    • p值：当零假设为真时，我们以零假设的参数建立正态分布（根据中心极限定理，当样本数量和抽样次数足够大时，抽样分布趋于正态分布），在该正态分布中观察到样本统计量甚至是更极端值（也就是偏向备则假设）的概率。

      若这个概率很大，比如说p = 1，那么就表示样本统计量在按照零假设模拟的正态分布内，我们就不能拒绝零假设；

      若这个概率很小，比如说 p < 0.05，那么在我们模拟的正态分布中观察到样本统计量的概率就是一个小概率事件，我们就可以拒绝零假设；

      若p值等于0.05，可增加样本容量，重新进行抽样检验。

有什么

  • 假设检验的基本思想

    • 逻辑上的反证法：我们先假设原命题（零假设H0）成立，然后推出明显矛盾的结果，证明原命题不成立，则我们的所证命题（备择假设H1）成立。
    • 小概率事件：概率很小的随机事件再一次随机实验中可以认为几乎是不会发生的，这就是小概率事件，我们证明零假设H0不成立，就是利用的小概率事件。

    假设检验的基本思想可以归纳为：我们把不想要的结果（即零假设H0）假设成立，然后利用样本计算出该假设成立时的概率（即支持该假设的概率，也就是p-value），如果这个概率小于显著性水平α（一般的为0.05），那么就可以说明零假设是小概率事件，可以拒绝，就证明了我们想要的结果（即备择假设H1）成立，可以表述为：在显著性水平α下拒绝原假设。

    试着理解一下上面这段话，如果理解不了，可以看看怎么用，会有详细的分步讲解。

  • 进行多次假设检验的校正

    • Bonferroni Correction：是一种降低多重比较时第一类错误的矫正方法，举例说明该用法：如果你想在 20 个假设检验中把 I 类错误率维持在 1%，邦弗朗尼 校正率应为 0.01/20 = 0.0005。你应该使用这个新比率作为显著性水平α，对比每 20 个检验的 p 值，再做出决定。

怎么用

  • 建立假设： 一般的都是均值或和与某数值之间的关系。示例如下：

$$
H_0:\mu \leqslant 7
$$

$$
H_1:\mu > 7
$$

  • 进行多次重复取样（自助法）
1
2
3
4
5
6
7
8
#从原数据集中取样，样本容量要大于30
sample_df = df.sample(100)
#新建列表
means = []
#循环取样，并计算均值，存贮在列表中
for _ in range(10000):
    bootsample = sample_df.sample(100,replace = True)#设置重复取样
    means.append(bootsample.height.mean())#计算数据集中height变量的均值
  • 构建零假设的正态分布（因为根据中心极限定理可知，当样本容量足够大，取样次数足够多时，均值的抽样分布近似于正态分布）
1
2
3
4
#计算抽样分布的标准差
null_std = np.std(means)
#构建正态分布
null_vals = np.random.normal(7,null_std,10000)#三个参数依次为正态分布的均值、标准差和取值数量，其中均值即为零假设设置的值。
  • 计算p值
1
2
3
4
#计算原始样本的均值
sample_mean = sample_df.height.mean()
#计算支撑原假设的概率，即p值。计算由原假设构建的正态分布（均值为7）大于样本统计量的概率。
p_value = (null_vals > sample_mean).mean()

若零假设为：u ≥ 7，则p_value = (null_vals < sample_mean ).mean();

若零假设为：u = 7，则p_value = (null_vals < sample_mean).mean() + (null_vals > null_mean + (null_mean - sample_mean) ).mean()

线性回归

基本概念

线性回归是属于机器学习中监督学习范畴的一种简单预测算法。我们通过查看两个定量变量之间是否存在线性关系，来进行预测。一般使用散点图对变量之间的关系进行可视化。

  • 反应变量就是你想进行预测的变量，其实也就是因变量(y)；

  • 解释变量就是你用于预测的变量，其实也就是自变量(x)。

  • 相关系数：最常用的就是皮尔逊相关系数，用r表示，取值范围为[-1,1]，正值表示正相关，负值表示负相关，绝对值越大，相关性就越强。在描述相关性强弱时，可以参考如下取值范围：

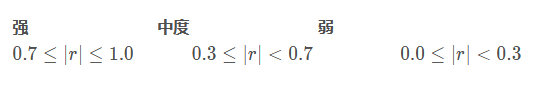
    imFK0K.png

    关于更多更详细的相关系数的知识，请戳统计学之三大相关性系数，博主写得深入浅出，而且有很多浅显易懂的例子，感兴趣的话可以看看。

方程

  • 方程模型

线性回归的方程模型就是一元一次方程，如下所示：

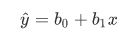
ila641.png

b0表示截距，也就是回归线与y轴交点的y坐标；

b1表示斜率，也就是回归线的倾斜程度；

y^ 表示回归线反应变量的预测值，并不是确切的数据集中的y值。

  • 拟合回归线

拟合回归线时我们采用的主要算法叫做 最小二乘法，即通过回归线得到的预测反应变量值与实际反应变量之差最小时的那条就是最佳拟合回归线，其原理公式可以表示为：

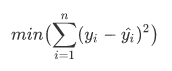
ilag9x.png

编程实现

在python中我们需要调用statsmodels包来拟合回归线：

1
2
3
4
5
6
7
8
9
10
11
# 加载statsmodels包
import statsmodels.api as sm
#注意一定不要忘了截距
df['intercept'] = 1
# 构建变量模型及其拟合
# y为因变量，X表示单个或多个自变量（其中要包含截距），例如 df[["intercept", "area"]] 包括了截距和面积两个变量
lm = sm.OLS(y, X) 		
result = lm.fit()

# 获取最终的拟合模型报告
print(result.summary())

在建立模型时，一般情况下都是需要手动添加截距（一般为常数 1）， 想了解更多，可以查阅Statcon: Why we need the intercept或者When is it ok to remove the intercept in a linear regression model? - Cross Validated

参数和结果解释

  • coef：对应变量的参数值
  • std err：标准误差
  • t：统计检验值
  • P>|t| ：这个是对应的 p 值，它的零假设为该变量的参数值等于0，可以指示该变量是否有利于预测反应变量，也能用于比较多个变量中哪个更重要。
  • R-squared ：即决定系数，它是相关系数的平方。取值范围在[0,1]，值越大，拟合效果就越好，这个值的统计意义可以简单解释为此次拟合中的解释变量能有多少百分比的可能去解释反应变量。

多元线性回归

基本概念

多元线性回归就是由多个自变量去预测因变量的方法，其模型方程与简单线性回归基本一致，只不过是将单自变量变为了多个自变量的矩阵，如下所示：

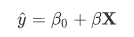
ilaRgK.png

其中X就是多个自变量的矩阵。

编程实现

在Python中的编程实现步骤也如简单线性回归类似，别忘了要定义一个截距

1
2
3
4
5
6
7
8
9
10
11
# 加载statsmodels包
import statsmodels.api as sm
#注意一定不要忘了截距
df['intercept'] = 1
# 构建变量模型及其拟合
# y为因变量，X表示多个自变量的矩阵（其中要包含截距），例如 df[["intercept", "area","bedroom", "bathroom"]] 包括了截距和面积、卧室数量、洗手间数量四个变量
lm = sm.OLS(y, X) 		
result = lm.fit()

# 获取最终的拟合模型报告
print(result.summary())

参数和结果解释

这里和简单线性回归是一致的，只不过在解释单个自变量与因变量之间的关系时，需要加上一句“在其它变量不变的情况下……”

处理分类变量

  • 思路

处理分类变量的一个思路就是将其转化为虚拟变量，也就是将各个分类变量单独成列，然后把观察行对应的分类变量量化为0（可理解为“否”）和1（可理解为“是”）作为该列的元素，再进行拟合处理。

在拟合处理时，我们添加的虚拟变量的数量应该为原数据集中的虚拟变量总数减一。

因为要计算最佳拟合系数时，需要用到变量矩阵的转秩，而判断矩阵是否可逆的充分必要条件就是这个矩阵是满秩的，又因为我们的虚拟变量矩阵中每一个变量都可以由其他变量推导而来，所以必须要舍弃一列才能确保变量矩阵为满秩。【感兴趣可以去可汗学院补一补线性代数知识】

  • 方法

使用pandas中的get_dummies函数来进行虚拟变量的转换

1
2
#对neighborhood列进行量化，并将结果存储在df数据集的A/B/C三个新列中
df[['A','B','C']] = pd.get_dummies(df['neighborhood'])

注意：get_dummies函数输出结果的默认排序为字典顺序（即a-z），所以在进行新列储存时，一定要注意原始变量中的分类与虚拟变量列一一对应。

  • 结果解释

还是以ABC三个分类变量来假设，我们以C作为基准变量（也就是删除的那列），那么在显示的结果中：

coef
Intercept i
A a
B b

1.Intercept的coef表示：如果分类为C的话，因变量即为i；

2.A的coef表示：如果分类为A的话，因变量为i+a;

3.B的coef表示：如果分类为B的话，因变量为i+b。

潜在问题

这部分课程中给了很多额外资料的链接，理论性很重，不太好啃，建议等通关后复盘的时候试着看一看。

多重共线性现象和分析

如果我们的自变量彼此相关，就会出现多重共线性。多重共线性的一个主要问题在于：它会导致简单线性回归系数偏离我们想要的方向。要判断是否有多重共线性，最常见的办法是借助散点图或 **方差膨胀因子 (即 VIF)**。

  • 散点图

散点图比较好理解，使用之前提到过的seaborn中的pairplot能很直观的看出各个变量之间的相关性。代码如下：

1
2
import seaborn as sns
sns.pairplot(df[["col_1", "col_2", "col_3"]])
  • 方差膨胀因子

方差膨胀因子(Variance Inflation Factor，VIF)是指解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比。具体的计算方法如下（计算不做要求，但要理解）

假若有X1 、X2 、X3三个自变量，X1的vif计算：
1.x1对常数项（截距）、x2、x3做多元线性回归，求出R^2
2.则变量X1的VIF＝1/(1-R^2)
3.同理计算出变量X2和X3的VIF。

它是指示多元线性回归中多重共线性严重与否的指标，VIF越大，多重共线性就越严重。

经验判断方法表明：

当0<VIF<10，不存在多重共线性；

当10≤VIF<100，存在较强的多重共线性；

当VIF≥100，存在严重多重共线性。

所以我们在处理的时候，就要去除VIF超过10的最不感兴趣的变量。

在python中的编程实现如下：

1
2
3
4
5
6
7
8
9
10
# 计算 VIF 需要使用 statsmodel 包
from statsmodels.stats.outliers_influence import variance_inflation_factor
from patsy import dmatrices	

# 筛选出作线性回归的变量（截距不要加）
y, X = dmatrices('col_y ~ col_1 + col_2 + col_3', df, return_type='dataframe')
vif = pd.DataFrame()
# 使用 variance_inflation_factor 来计算 VIF，并储存在vif DataFrame中
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])] 
vif["features"] = X.columns

【选修】高阶项

高阶项就是在回归模型中添加诸如x^2,x^3,x1·x2等变量，获取的方式可以直接使用df[‘col_1’]进行高阶计算即可。

关键是在于观察变量之间的散点图，来确定是否需要添加高阶项。

  • 二阶、三阶的函数曲线很有辨识度，观察他们拐几个弯就可以；
  • 交叉项的话，就看两自变量各自与因变量之间的回归线，如果回归线几乎平行，那就不必添加交叉项；

注意：如果确定要添加某变量的高阶项，一定要确保该变量也要添加进去。

之后的24-33节也是选修，而且给了Udacity一套免费的机器学习入门课程，建议通关后再来复盘。

逻辑回归

逻辑回归就是对分类变量进行预测的方法，尤其是对二分类问题（非1即0），比如说是否使用优惠券，是否存在贷款逾期问题等等。

方程

逻辑回归的方程模型就是sigmoid函数：

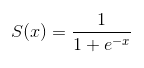
iKlzUe.png

结合二分类问题的概率，做对数变换可得：

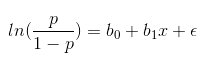
izcBWD.png

如上p/(1-p)即为事件的机会比，在该问题中，能预测范围在0到1之间。

编程实现

编程实现与线性回归类似，只不过将最小二乘法（OLS）替换成了逻辑回归（Logit）:

1
2
3
4
5
6
7
8
9
10
11
# 加载statsmodels包
import statsmodels.api as sm
#注意一定不要忘了截距
df['intercept'] = 1
# 构建变量模型及其拟合
# y为二分类变量，X表示多个自变量的矩阵（其中要包含截距），例如 df[["intercept","duration"]] 包括了截距和持续时间
lm = sm.Logit(y, X) 		
result = lm.fit()

# 获取最终的拟合模型报告
print(result.summary())

参数和结果解释

  • coef：对应变量的系数
  • std err：标准误差
  • t：统计检验值
  • P>|t| ：这个是对应的 p 值，可以指示该变量是否有利于预测反应变量，也能用于比较多个变量中哪个更重要。

在这里我们并不关注截距，而重点关注各个解释变量。

在进行结果解释时我们常说：

在保持其他变量不变的情况下，

  • （对于数值变量）该变量每增加一个单位，那么作为y的分类变量则增大e^coef倍；
  • （对于分类变量）该变量为它的对立时，作为y的分类变量发生的几率为该变量基础的e^coef倍。

【选修】模型评估

之后的课程已经是机器学习入门阶段的范畴，可以等通关后，再去研究。（建议先开始免费的机器学习课程，再结合本章内容复盘看，更有助于你理解）

总结

本周导学的内容较难，理解起来也比较困难，对于置信区间和假设检验两节，大家可以再额外补充一些统计学方面的相关知识，更有助于你理解；对于回归知识，建议多看几遍教学视频再结合例题，在实践中不断尝试去理解，大家加油！下周就要开始项目四了，阶段性的胜利就在前方！