Allen's Blog

体制山下的泼猴

0%

Python Code of Mini-Batch Gradient Descent

发表于 更新于 分类于 阅读次数： Valine：

概述

Mini-Batch Gradient Descent是介于batch gradient descent（BGD）和stochastic gradient descent（SGD）之间的一种线性回归优化算法，它是将数据分为多个小的数据集（batches），每个数据集具有大致相同的点数，然后在每个数据集中应用Absolute Trick或者是Square Trick算法，来更新回归系数。

它的运算速度比BSD快，比SGD慢；精度比BSD低，比SGD高。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)

def MSEStep(X, y, W, b, learn_rate = 0.001):
    """
    This function implements the gradient descent step for squared error as a
    performance metric.
    
    Parameters
    X : array of predictor features
    y : array of outcome values
    W : predictor feature coefficients
    b : regression function intercept
    learn_rate : learning rate

    Returns
    W_new : predictor feature coefficients following gradient descent step
    b_new : intercept following gradient descent step
    """
    
    # compute errors
    # the squared trick formula 
    y_pred = np.matmul(X, W) + b #Attention:the order of X and W
    error = y - y_pred
    #y_pred is a 1-D array,so is the error
    
    # compute steps
    W_new = W + learn_rate * np.matmul(error, X) #Attention:the order of X and error
    b_new = b + learn_rate * error.sum() 
    return (W_new, b_new)

def miniBatchGD(X, y, batch_size = 20, learn_rate = 0.005, num_iter = 25):
    """
    This function performs mini-batch gradient descent on a given dataset.

    Parameters
    X : array of predictor features
    y : array of outcome values
    batch_size : how many data points will be sampled for each iteration
    learn_rate : learning rate
    num_iter : number of batches used

    Returns
    regression_coef : array of slopes and intercepts generated by gradient
      descent procedure
    """
    n_points = X.shape[0]
    W = np.zeros(X.shape[1]) # coefficients
    b = 0 # intercept
    
    # run iterations
    #hstack为水平堆叠函数 为什么要堆叠呢？
    #类似zip，可以实现for W,b in regression_coef:print W,b来提取W和b
    regression_coef = [np.hstack((W,b))]
    for _ in range(num_iter):
        #从0-100中随机选择batch_size个数，作为batch
        batch = np.random.choice(range(n_points), batch_size)
        #按照batch从X中选出数据
        X_batch = X[batch,:]#为2-D矩阵
        y_batch = y[batch]#为1-D数组
        W, b = MSEStep(X_batch, y_batch, W, b, learn_rate)
        regression_coef.append(np.hstack((W,b)))
    
    return (regression_coef)

if __name__ == "__main__":
    # perform gradient descent
    data = np.loadtxt('data.csv', delimiter = ',')
    X = data[:,:-1]#提取第一列，为2-D矩阵
    y = data[:,-1]#提取第二列，为1-D数组
    regression_coef = miniBatchGD(X, y)
    
    # plot the results  
    plt.figure()
    X_min = X.min()
    X_max = X.max()
    counter = len(regression_coef)
    for W, b in regression_coef:
        counter -= 1
         #color为[R,G,B]的列表，范围都在0-1之间，[0,0,0]为黑色，[1,1,1]为白色
        color = [1 - 0.92 ** counter for _ in range(3)]
        #绘制一条点(X_min,X_min * W + b)与点(X_max, X_max * W + b)之间的一条直线
        plt.plot([X_min, X_max],[X_min * W + b, X_max * W + b], color = color)
    plt.scatter(X, y, zorder = 3)
    plt.show()

结果

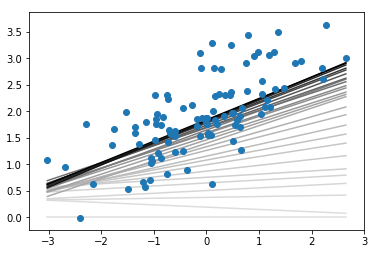
FldOgg.png

在结果中，颜色最浅的是最开始的回归线，最深的则为最终的回归线。

详解

理论知识参见Linear Regression 总结，这里只对代码中出现的新函数或新用法进行讲解。

numpy.matmul(a,b)

该函数用来计算两个arrays的乘积。

需要注意的是，由于a和b维度的不同，会使得函数的结果计算方式不同，一共三种：

  • 如果a和b都是2维的，则做普通矩阵乘法

    1
    2
    3
    a = [[1, 0], [0, 1]]
    b = [[4, 1], [2, 2]]
    np.matmul(a, b)
    1
    2
    3
    out:
    array([[4, 1],
           [2, 2]])

  • 如果a和b中有一个是大于2维的，则会将其理解为多个矩阵stack后的结果，进行计算时也会进行相应的拆分运算

    1
    2
    3
    a = np.arange(2*2*4).reshape((2,2,4))
    b = np.arange(2*2*4).reshape((2,4,2))
    np.matmul(a,b).shape
    1
    2
    out:
    (2, 2, 2)

    a被理解为2个2x4矩阵的stack

    1
    2
    3
    4
    5
    array([[[ 0,  1,  2,  3],
            [ 4,  5,  6,  7]],

           [[ 8,  9, 10, 11],
            [12, 13, 14, 15]]])

    b被理解为2个4x2矩阵的stack

    1
    2
    3
    4
    5
    6
    7
    8
    9
    array([[[ 0,  1],
            [ 2,  3],
            [ 4,  5],
            [ 6,  7]],

           [[ 8,  9],
            [10, 11],
            [12, 13],
            [14, 15]]])

    np.matmul(a,b)会将a中的两个矩阵与b中的两个矩阵对应相乘，每对相乘的结果都是一个2x2的矩阵，所以结果就是一个2x2x2的矩阵。

  • 如果a或b有一个是一维的，那么就会为该一维数组补充1列或1行，进而提升为二维矩阵，然后用非补充行或列去和另外一个二维矩阵进行运算，得到的结果再将补充的1去掉。（这个是最难理解的，可以多测试下，用代码结果理解）

    1
    2
    3
    a = [[1, 0], [0, 1]]
    b = [1, 2]
    np.matmul(a, b)
    1
    2
    out:
    array([1, 2])

    a是一个2x2的矩阵，b是一个shape为(2,)的一维数组，那么matmul的计算步骤如下：

    • 计算中，矩阵a在前，数组b在后，所以需要让a的列数与升维之后b矩阵的行数相等
    • 所以，升维后b矩阵的shape应为(2,1)，这个1添加到了列上
    • 进行矩阵乘法计算，得到shape为(2,1)，这时候再将这个1去掉
    • 最终结果的shape为(2,)，变为一维数组

    我们试着将a与b的顺序对调，看一下matmul是怎么计算的：

    • 对调后，数组b在前，矩阵a在后，需要将升维后b矩阵的列数与矩阵a的行数相等
    • 所以，升维后b矩阵的shape应该为(1,2)，这个1添加到了行上
    • 进行矩阵乘法，得到的shape为(1,2)，将这个1去掉
    • 最终结果的shape为(2,)，变为一维数组

numpy.hstack()

我们先来看看numpy.stack()函数。

  • 函数用法为：numpy.stack(arrays,axis = 0)
  • 第一个参数为arrays，可以输入多维数组或者列表，也可以输入由多个一维数组或列表组成的元组
  • 第二个参数为axis，输入数字，决定了按照arrays的哪个维度进行stack。比如说，输入的arrays的shape为(3,4,3)，那么axis = 0/1/2就分别对应arrays的组/行/列。

这个函数中的axis有些抽象，我们看具体示例：

  • 定义了一个列表

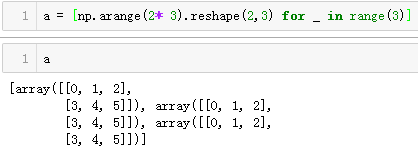
F1PSIS.png

结果的排版有点问题，为了方便后面对照，把结果对齐如下：

1
2
3
4
5
[
    array([[0,1,2],[3,4,5]]),
    array([[0,1,2],[3,4,5]]),
    array([[0,1,2],[3,4,5]])
]

  • axis = 0，则按照第0个维度组进行堆叠，即：

    F1PqFU.png

    结果为：

    F1PLYF.png

  • axis = 1，则按照第1个维度行进行堆叠，即：

    F1Pvl9.png

    结果为：

    F1PzO1.png

  • axis = 2，则按照第二个维度列进行堆叠，即：

    F13zdO.png

    结果为：

    1544074512445

    这个基本很少用到。

**numpy.hstack()**函数就是horizontal（水平）方向的堆叠，示例：

F18qAS.png

**numpy.vstack()**函数就是在垂直方向堆叠。

ndarray的切片

一维ndarray的切片方式和list无异，这里主要讲一下二维矩阵的切片方法。

  • 矩阵切片
1
2
a = np.arange(4*4).reshape(4,4)
print(a)
1
2
3
4
5
out:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])
1
a[:,:-1]
1
2
3
4
5
out:
array([[ 0,  1,  2],
       [ 4,  5,  6],
       [ 8,  9, 10],
       [12, 13, 14]])

这里可以看出，我们筛选了a矩阵中前三列的所有行，这是如何实现的呢？

切片的第一个元素:表示的是选择所有行，第二个元素:-1表示的是从第0列至最后一列（不包含），所以结果如上所示。

再看一个例子：

1
a[1:3,:]
1
2
3
out:
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

筛选的是第2-3行的所有列。

  • 一个常用的切片

以列的形式获取最后一列数据：

1
a[:,3:]
1
2
3
4
5
out:
array([[ 3],
       [ 7],
       [11],
       [15]])

以一维数组的形式获取最后一列数据：

1
a[:,-1]
1
2
out:
array([ 3,  7, 11, 15])

上面两种方法经常会用到，前者的shape为(4,1)，后者为(4,)。

matplotlib相关

  • color

    代码中涉及到的语句为：

    1
    color = [1 - 0.92 ** counter for _ in range(3)]

    matplotlib中的color可以输入RGB格式，即[R,G,B]，这里值得注意的是它们的取值范围都在0到1之间，其中[0,0,0]为黑色，[1,1,1]为白色。

    在如上语句中，列表由三个相等的数值元素组成，保证了颜色为白-灰-黑，数值随着counter的减小，由1趋近于0，反映在可视化上就是颜色由白逐渐变黑。

    这真是一个画渐变过程的好方法呀！！！

  • plot([x_1,x_2],[y_1,y_2])

    这里就是两点式绘图，根据点(x_1,y_1)和点(x_2,y_2)画一条直线。

  • zorder

    也就是z-order，类似于PS里面的图层顺序，下面的图层会被上面的图层遮挡。

    参考Zorder Demo中队zorder的介绍，可以知道，zorder越大，图层越靠上，所以在上面的代码中，我们在scatter中设定zorder为3，也就是最上层，这样就可以保证渐变的回归线不会压在散点图上面了。

    F1JYiF.png